JAVA流程控制01——用户交互Scanner和scanner的进阶使用
本文共 506 字,大约阅读时间需要 1 分钟。
JAVA流程控制——用户交互Scanner和scanner的进阶使用
Scanner对象
通过Scanner类的next()与nextLine()获取输入的字符串,在读取前我们一般需要使用hasNext()与hasNextLine()判断是否还有输入的数据
next()与nextLine()的区别
next():
- 一定要读取到有效字符才可以结束输入
- 对输入有效字符之前遇到的空白,next()方法会自动将其去掉
- 只有输入有效字符后才将其后面输入的空白作为分隔符或者结束符
- next()不能得到带有空格的字符串


nextLine():
- 以Enter为结束符,也就是说nextLine()放发返回的是输入回车
之前的所有字符
- 可以获得空白
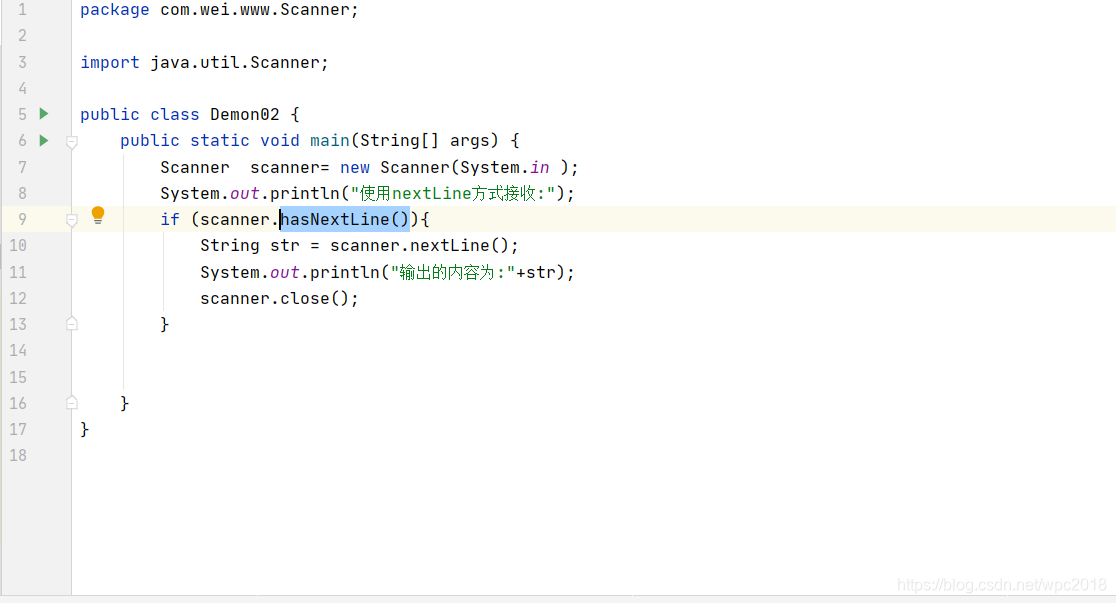
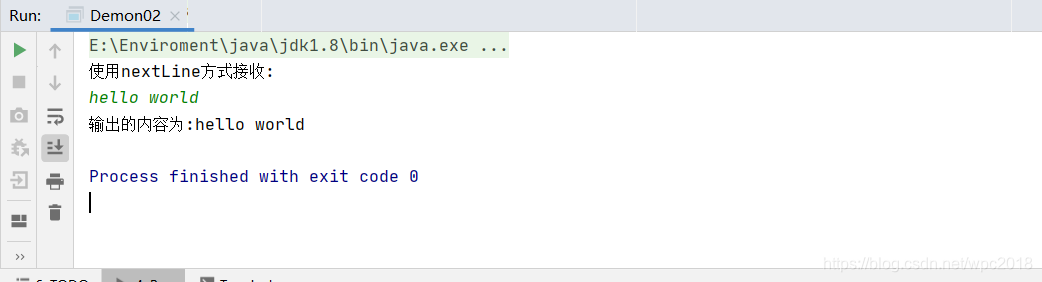
注意:凡是属于IO(输入输出)流的类如果不关闭会一直占用资源,要要用完就关掉。列如scanner类,使用完后要关闭scanner.close();
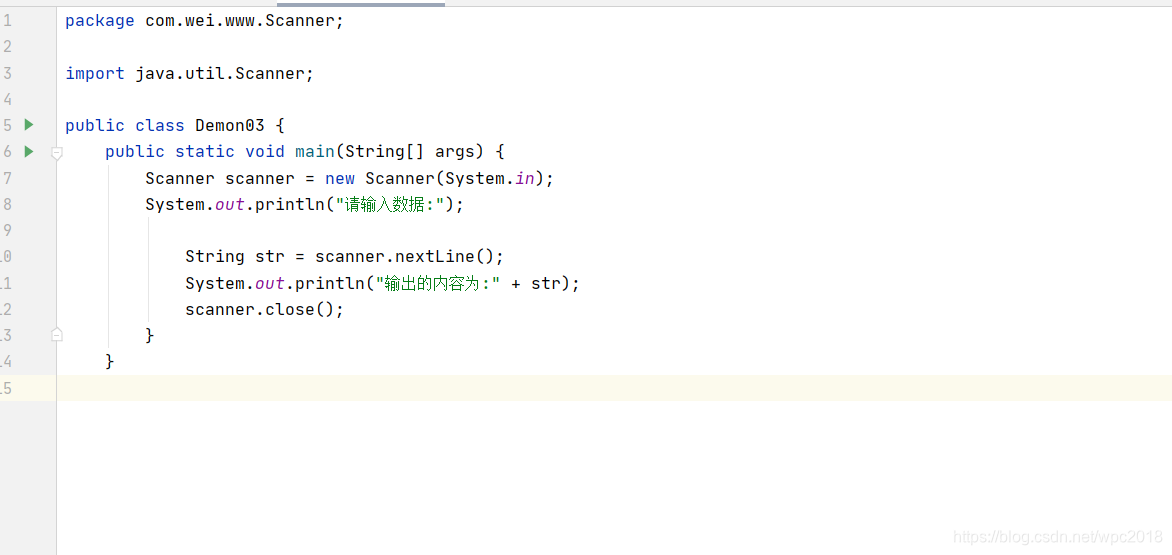
拓展:不加判断直接使用scanner类来获取输入的字符
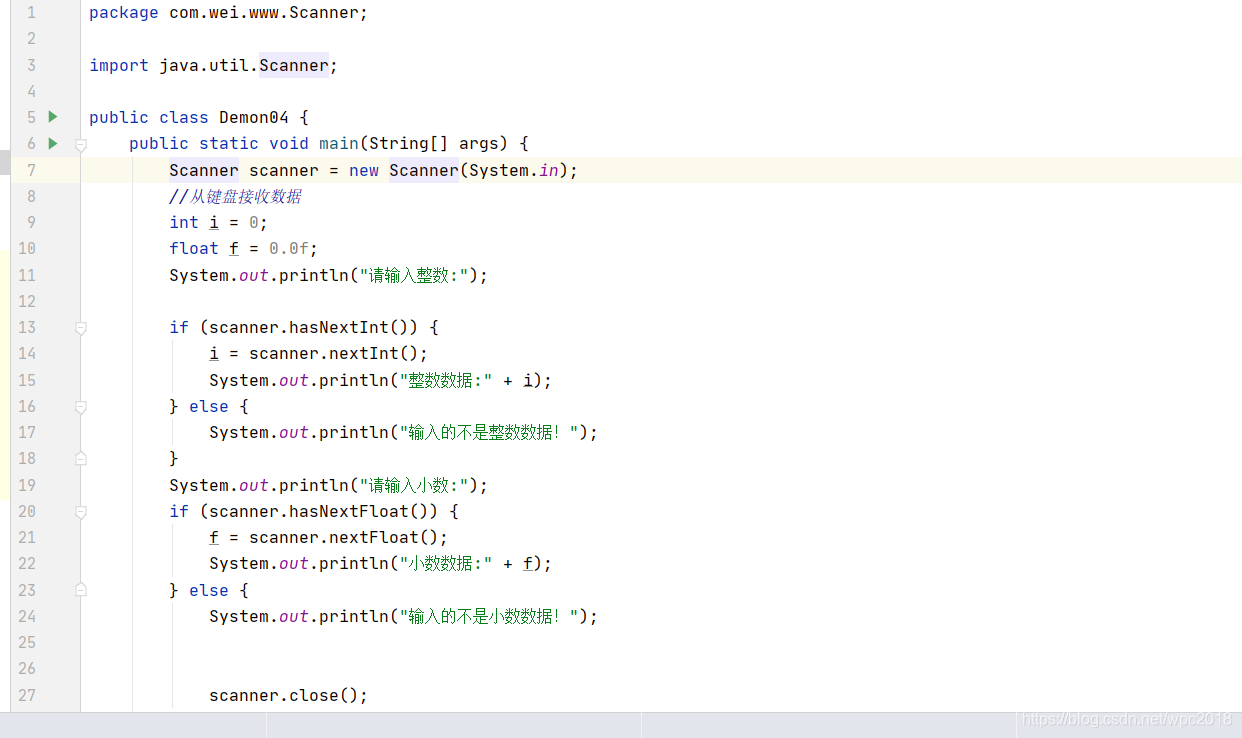
Scanner的进阶使用
输入一个数,判断输入的是整数还是小数
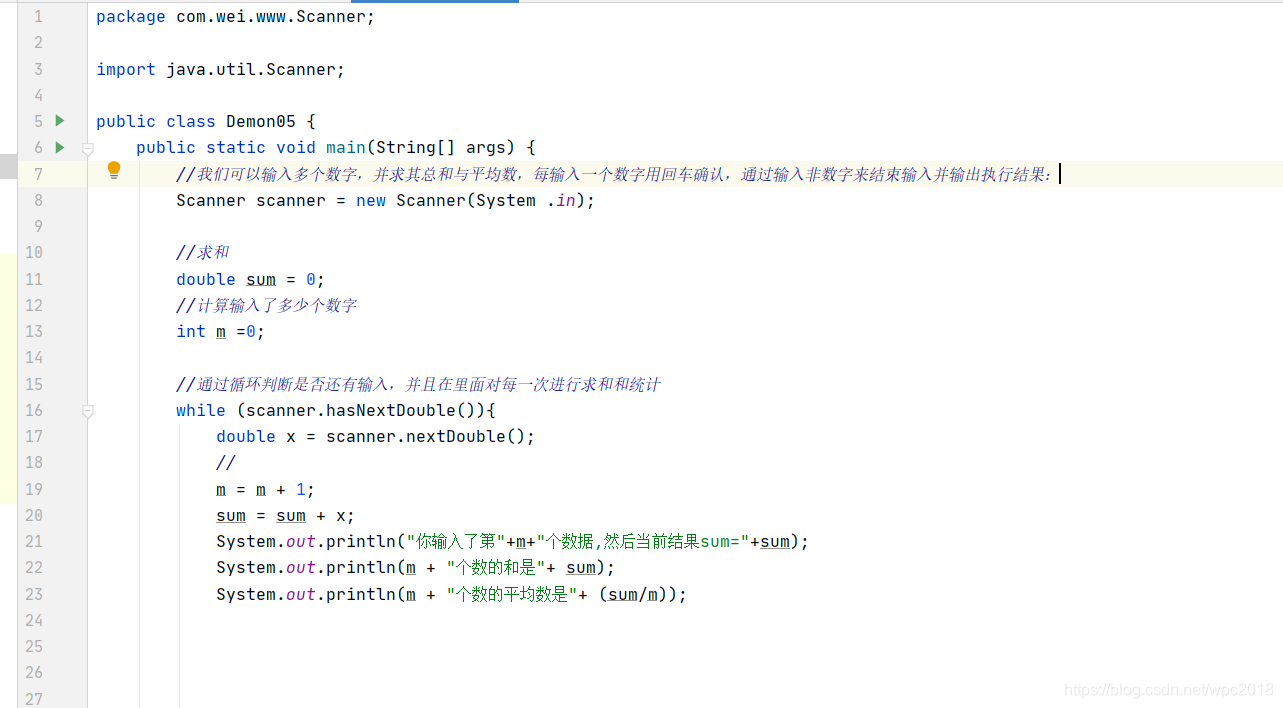
我们可以输入多个数字,并且求其总和与平均数,每输入一个数字用回车确认,通过输入非数字来结束并输出执行结果:
转载地址:http://oqov.baihongyu.com/
你可能感兴趣的文章